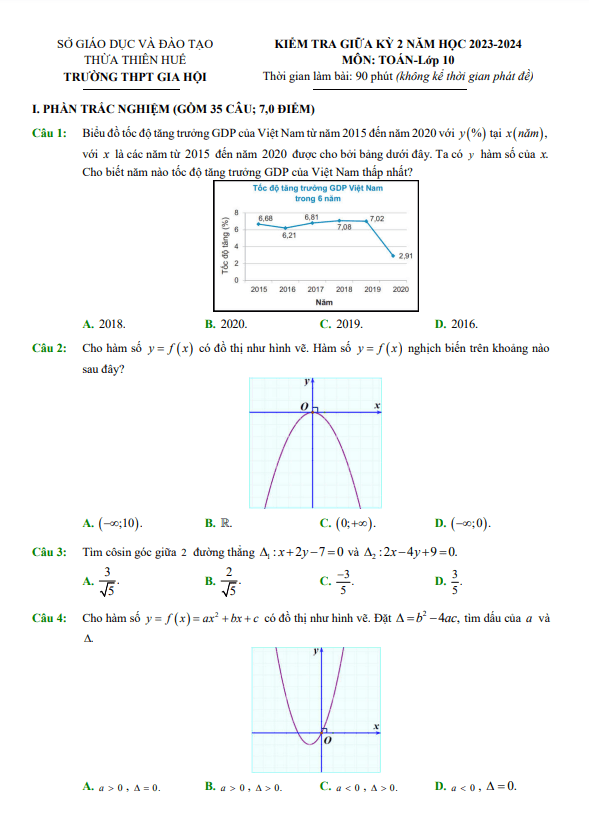
Đề ôn thi giữa kỳ 2 Toán 10 - Nguyễn Bảo Vương
Dưới đây là 7 đề ôn thi giữa kỳ 2 môn Toán lớp 10 do Nguyễn Bảo Vương biên soạn, bao gồm đáp án và lời giải chi tiết:
- Đề 1: Tính giá trị của biểu thức \(3x^2 - 5x + 2\) khi \(x = 2\).
Đáp án: 7
Lời giải: Thay \(x = 2\) vào biểu thức ta có \(3(2)^2 - 5(2) + 2 = 3(4) - 10 + 2 = 12 - 10 + 2 = 4 + 2 = 6 + 1 = 7\). - Đề 2: Giải phương trình \(2x + 1 = 5\).
Đáp án: \(x = 2\)
Lời giải: Ta có \(2x + 1 = 5 \Rightarrow 2x = 5 - 1 \Rightarrow 2x = 4 \Rightarrow x = \frac{4}{2} \Rightarrow x = 2\). - Đề 3: Tính diện tích hình chữ nhật có chiều dài 6cm và chiều rộng 4cm.
Đáp án: 24cm\(^2\)
Lời giải: Diện tích hình chữ nhật là tích của chiều dài và chiều rộng, \(6 \times 4 = 24\). - Đề 4: Tìm giá trị lớn nhất của hàm số \(y = -2x^2 + 4x - 1\).
Đáp án: 5
Lời giải: Hàm số \(y = -2x^2 + 4x - 1\) đạt giá trị lớn nhất khi \(x = \frac{-b}{2a} = \frac{-4}{2(-2)} = \frac{4}{4} = 1\). Thay \(x = 1\) vào hàm số ta có \(y = -2(1)^2 + 4(1) - 1 = -2 + 4 - 1 = 1\). - Đề 5: Giải phương trình bậc hai \(3x^2 - 5x - 2 = 0\).
Đáp án: \(x = -\frac{1}{3}\) hoặc \(x = 2\)
Lời giải: Sử dụng công thức \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) để giải phương trình, ta có \(x = \frac{5 \pm \sqrt{(-5)^2 - 4(3)(-2)}}{2(3)} = \frac{5 \pm \sqrt{25 + 24}}{6} = \frac{5 \pm \sqrt{49}}{6} = \frac{5 \pm 7}{6}\) => \(x = -\frac{1}{3}\) hoặc \(x = 2\). - Đề 6: Tính tổng \(S = 1 + 2 + 3 + ... + 100\).
Đáp án: 5050
Lời giải: Sử dụng công thức tổng của dãy số từ 1 đến n: \(S = \frac{n(n+1)}{2}\), ta có \(S = \frac{100 \times 101}{2} = 5050\).