Chứng minh tứ giác nội tiếp đường tròn

Chứng minh tứ giác nội tiếp đường tròn

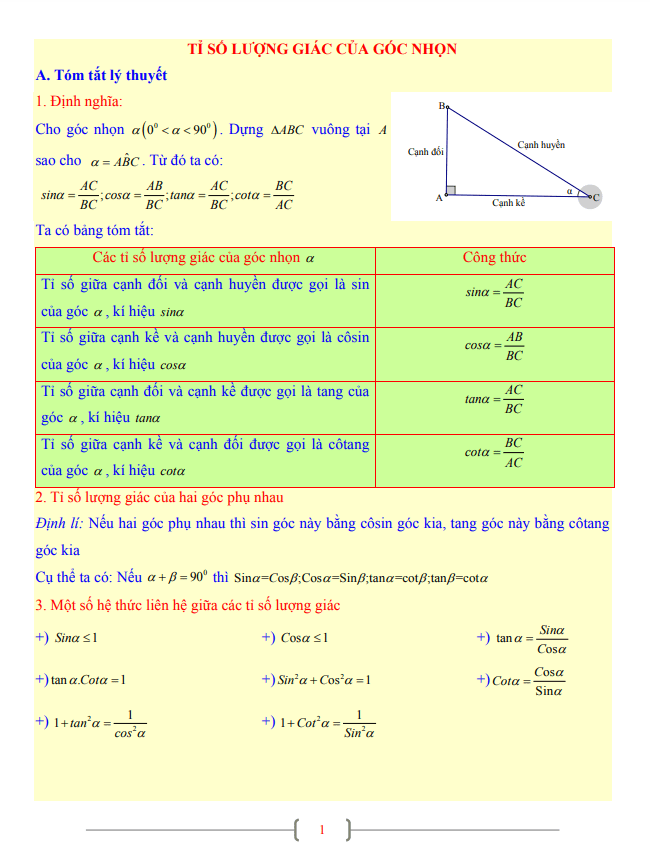
Chứng minh tứ giác ABCD nội tiếp đường tròn (O) khi và chỉ khi tứ giác đó có tổng các góc đối diện bằng 180 độ.

Giả sử tứ giác ABCD nội tiếp đường tròn (O), ta có:

• Góc ABC + góc CDA = 180 độ (vì hai góc này là góc đối diện và cùng nằm trên cùng một dây)
• Góc ABD + góc CAD = 180 độ (vì hai góc này là góc đối diện và cùng nằm trên cùng một dây)

Vậy tổng các góc đối diện của tứ giác ABCD là:

Góc ABC + góc ABD + góc CAD + góc CDA = 360 độ

Ngược lại, nếu tứ giác ABCD có tổng các góc đối diện bằng 360 độ, ta chứng minh được tứ giác đó nội tiếp đường tròn (O).

Đây chính là cách chứng minh tứ giác nội tiếp đường tròn dựa trên tính chất của các góc trong tứ giác và đường tròn. Việc này giúp chúng ta dễ dàng nhận biết và xác định tứ giác nội tiếp đường tròn trong các bài toán về hình học không gian.