Chuyên đề một số hệ thức về cạnh và góc trong tam giác vuông
Trong toán học, tam giác vuông là một trong những dạng tam giác cơ bản và quan trọng nhất. Trong tam giác vuông, chúng ta có ba cạnh và ba góc. Dưới đây là một số hệ thức và quy tắc quan trọng về cạnh và góc trong tam giác vuông:
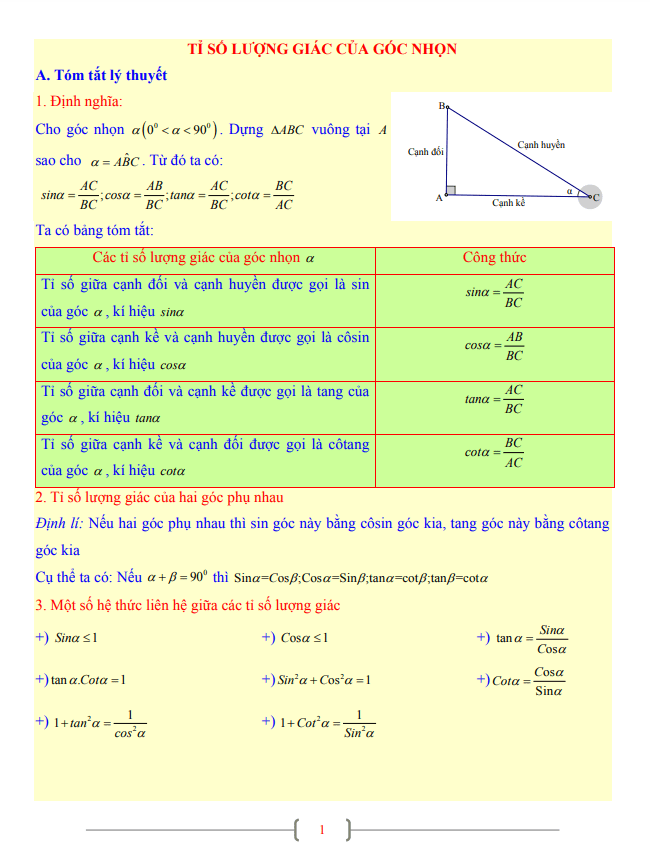
1. Định lý Pythagore: Trong tam giác vuông, bình phương của độ dài cạnh huyền bằng tổng bình phương của hai cạnh góc vuông. Cụ thể, nếu gọi cạnh huyền là c, và hai cạnh góc vuông lần lượt là a và b, ta có: c2 = a2 + b2.
2. Tính chất của các góc trong tam giác vuông: Trong tam giác vuông, một góc bằng 90 độ, gọi là góc vuông. Hai góc còn lại gọi là góc nhọn và góc tù. Góc nhọn lớn hơn góc tù.
3. Hệ thức sin, cos và tan trong tam giác vuông: Trong tam giác vuông, ta có các hệ thức quan trọng liên quan đến sin, cos và tan của các góc trong tam giác vuông. Ví dụ, sin(α) = a/c, cos(α) = b/c, tan(α) = a/b, với α là một trong ba góc của tam giác vuông, và a, b, c lần lượt là các cạnh của tam giác.
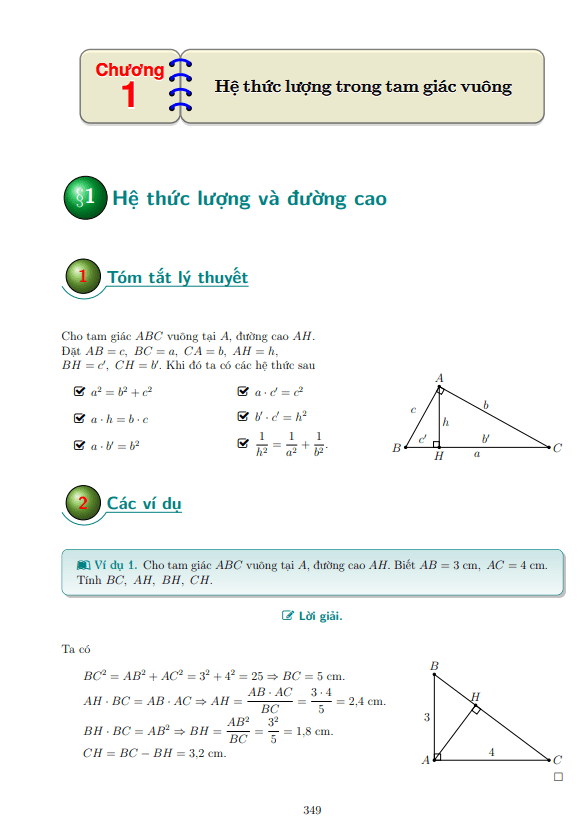
4. Định lý thứ nhất của Euclid: Trong tam giác vuông, nếu kẻ đường cao từ góc vuông xuống cạnh huyền, thì tam giác tạo thành sẽ tự động trở thành hai tam giác vuông nhỏ khác.
Trên đây là một số hệ thức và quy tắc quan trọng về cạnh và góc trong tam giác vuông. Hiểu và áp dụng chúng sẽ giúp bạn giải quyết các bài toán liên quan đến tam giác vuông một cách chính xác và nhanh chóng.